Die Entropie als mengenartige Grösse und Energieträger
Sadi Carnot hat im Jahr 1824 in seinen « Réflexions sur la puissance motrice du feu » („Betrachtungen über die bewegende Kraft des Feuers“) grundsätzliche Überlegungen zur maximal möglichen Nutzbarmachung von Wärme (oder Wärmestoff, wie dies in der deutschen Übersetzung benennt wird) zur Erzeugung von bewegender Kraft, bzw. Prozessleistung wie wir dies heute bezeichnen wollen, gemacht.
Dabei hat er die Wirkung des über ein Temperaturgefälle fliessenden Wärmestoffs mit jener des über eine Gefällsstufe fliessenden Wassers verglichen.
Zitat aus der deutschen Übersetzung:
Die bewegende Kraft des fallenden Wassers hängt von seiner Höhe und der Menge der Flüssigkeit ab; die bewegende Kraft der Wärme hängt gleichfalls von der Menge des angewendeten Wärmestoffes ab, und dem, was man seine Fallhöhe nennen könnte, und was wir in der That so nennen wollen, nämlich dem Temperaturunterschied der Körper, zwischen denen der Austausch des Wärmestoffes stattfindet.
Diese Analogie haben die Physikdidaktiker der Universität Karlsruhe wieder aufgegriffen und auf weitere Gebiete der Physik angewendet, daraus den Physikkurs (KPK) mit seinem Energieträgerkonzept entwickelt und dabei die Entropie als verständliche Grösse im Sinne des Wärmestoffes von Sadi Carnot neu vermittelt.
Nach dem Energieträgerkonzept des KPK wird die Energie immer zusammen mit einer anderen mengenartigen Grösse bewegt, ja von dieser getragen und in Prozessen von einer mengenartigen, extensiven Grösse zu einer anderen mengenartigen Grösse umgeladen, bzw. übertragen. Zu jeder mengenartigen Grösse gehört das Potential bzw. die Tragfähigkeit für Energie (intensive Grösse).
Fällt nun ein solcher Energieträger über eine zugehörige Potentialdifferenz, so trägt er nach dem Fall einen geringeren Energiestrom und diese Energiestrom-Differenz kann als Prozessleistung verfügbar gemacht werden.
Beispiel Wasserfall:
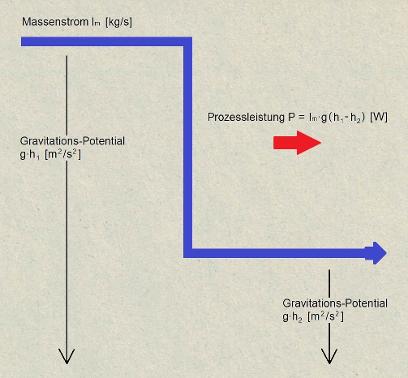
Ein Wasser-Massenstrom fliesst auf einer bestimmten Höhe im Gravitationsfeld und trägt dem entsprechend einen Energiestrom. Der mitgetragene Energiestrom ist direkt proportional zum Gravitations-Potential (g×h). Fällt der Massenstrom über eine Gefällsstufe, so trägt er dann auf dem unteren Potential einen entsprechend kleineren Energiestrom.
Die Energiestrom-Differenz (=Prozessleistung) kann durch einen technischen Prozess, verfügbar gemacht werden.
Wird die Prozessleistung nicht genutzt, wie es häufig vorkommt, so wird damit Entropie produziert und mit diesem erzeugten Entropiestrom die Energiestrom-Differenz vom Prozessort fortgetragen.
Wasserfall
Beispiel Entropiefall:
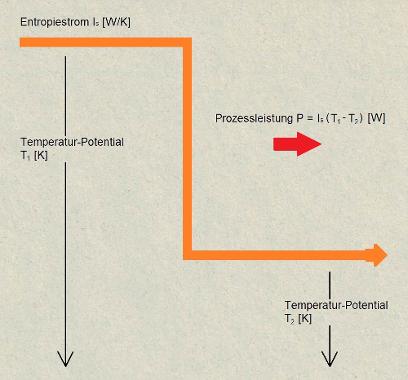
Ein Entropiestrom fliesst leitungsartig auf dem Potential der absoluten Temperatur (Kelvin) und trägt dem entsprechend einen Energiestrom. Der mitgetragene Energiestrom ist direkt proportional zum absoluten Temperatur-Potential. Fällt der Entropiestrom über ein Temperaturgefälle, so trägt er dann auf dem unteren Potential einen entsprechend kleineren Energiestrom.
Die Energiestrom-Differenz (=Prozessleistung) kann durch einen technischen Prozess verfügbar gemacht werden.
Wird die Prozessleistung nicht genutzt, wie es häufig vorkommt, so wird damit zusätzlich Entropie produziert und mit dem derart vergrösserten Entropiestrom der Gesamtenergiestrom fortgetragen.
Entropiefall
Herkunft des Begriffs Entropie
Erst nach Sadi Carnot wurde um die Mitte des neunzehnten Jahrhunderts die Energieerhaltung erkannt und formuliert, etwa durch Julius Robert Mayer, der 1841 seine Idee, dass Energie weder erschaffen noch vernichtet werden kann, veröffentlichte (erster Hauptsatz).
Gemäss einer Vortrags-Schrift von Rudolf Clausius aus dem Jahr 1865 hat William Thomson, der spätere Lord Kelvin, vorgeschlagen, den Begriff "Energie" für die umfassende Bezeichnung des "Wärme- und Werkinhaltes" eines Systems zu verwenden. Dieser William Thomson führte ausserdem in einer 1848 verfassten Arbeit zur Thermodynamik auch die später nach ihm benannte absolute Temperaturskala ein ("Kelvin" mit Nullpunkt bei minus 273.15 °C).
Rudolf Clausius schreibt in seinen Abhandlungen zur mechanischen Wärmetheorie, insbesondere auch in der bereits erwähnten, am 24. April 1865 vorgetragenen, von Verwandlungsinhalt und meint damit den Quotienten Wärme (Q)/Temperatur (T, absolut). Demnach schreibt er unter anderem auch im Sinne des zweiten Hauptsatzes, Zitat: die algebraische Summe aller bei einem Kreisprocesse vorkommenden Verwandlungen kann nur positiv oder als Grenzfall Null sein.
An einer anderen Stelle steht zur irreversiblen Wärmeleitung mit "positiver Verwandlung", Zitat: Wenn die Wärmemenge Q aus einem Körper von der Temperatur T1 in einen anderen von der Temperatur T2 übergeht, so hat diese Verwandlung den Aequivalenzwerth von Q(1/T2-1/T1).
In der Abhandlung von 1865 wird dann der neue Name für die Grösse mit dem Formelzeichen S eingeführt, Zitat: Da ich es aber für besser halte, die Namen derartiger für die Wissenschaft wichtiger Grössen aus den alten Sprachen zu entnehmen, damit sie unverändert in allen neuen Sprachen angewandt werden können, so schlage ich vor, die Grösse S nach dem griechischen Worte "die Verwandlung", die Entropie des Körpers zu nennen.
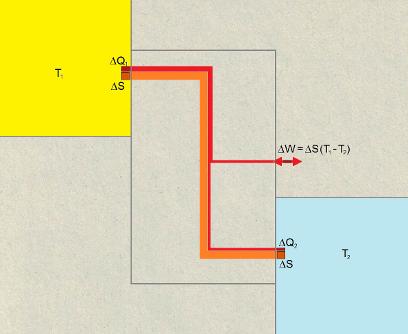
Beim idealen, reversiblen Vorgang geht die Entropie ∆S vom homogenen Körper mit der höheren Temperatur T1 leitungsartig in den "Wärme-Kraft-Prozess" und von da wieder leitungsartig in den homogenen Körper mit der tieferen Temperatur T2. Dabei wird die Prozessenergie ∆W verfügbar gemacht ("Wärme-Kraft-Maschine") oder beim umgekehrten Vorgang, wenn ∆S vom tieferen Temperatur-Potential T2 aufs höhere Potential T1 gefördert werden soll, wird die Prozessenergie ∆W aufgewendet ("Wärme-Pumpe"). Die Entropiemenge ∆S=∆Q/T bleibt unverändert und trägt eine entsprechend tiefere Energie-/Wärmemenge ∆Q2 in den, bzw. aus dem Körper mit der tieferen Temperatur T2, so dass die Energiebilanz stimmt: ∆W=∆Q1-∆Q2 oder umgeformt ∆W=∆S×(T1-T2).
Diese Idealprozesse verlaufen also isentrop und sind ein Massstab für technische Lösungen, aber in der Realität nicht erreichbar.
Bei der reinen Wärmeleitung, bei welcher sich gemäss Rudolf Clausius eine "positive Verwandlung", also eine Entropiezunahme ergibt, ist hingegen die ausgetauschte Wärmemenge ∆Q konstant. Die Entropiemenge ∆S wird durch die Entropieproduktion der ungenutzten Prozessenergie ∆W erhöht: ∆S2=∆S+∆W/T2 oder umgeformt ∆S2=∆S×T1/T2. Die Entropiezunahme von ∆S auf ∆S2, bzw. ausgeschrieben ∆S×(T1/T2 - 1) entspricht der Schreibweise von Rudolf Clausius, der den "Aequivalenzwerth der Verwandlung" mit ∆Q×(1/T2 - 1/T1) angibt und unter anderem dazu schreibt, Zitat: dass die Wärme nicht von selbst aus einem kälteren in einen wärmeren Körper übergehen kann (zweiter Hauptsatz), dass also ein typischer, realer Prozess mit Entropiezunahme nicht reversibel ist und nur in diese eine Richtung spontan abläuft.
Weitergehende Betrachtungen zu Entropie und Energie
Der isentrope Wirkungsgrad als objektives Mass zur Beurteilung der Qualität technischer Prozesse der Energieumladung

|
Isentroper_Wirkungsgrad.pdf Größe: 590,472 Kb Typ: pdf |
Spezielle Prozesse bei denen die innere Energie unverändert bleibt (isoenergetisch)

|
Isoenergetische_Prozesse.pdf Größe: 400,195 Kb Typ: pdf |